Una ecuación de primer grado o ecuación lineal es un planteamiento de igualdad, involucrando una o más variables a la primera potencia, que no contiene productos entre las variables, es decir, una ecuación que involucra solamente sumas y restas de una variable a la primera potencia. En el sistema cartesiano representan rectas. Una forma común de ecuaciones lineales es:
 representa la pendiente y el valor de
representa la pendiente y el valor de  determina la ordenada al origen (el punto donde la recta corta al eje y).
determina la ordenada al origen (el punto donde la recta corta al eje y).Las ecuaciones en las que aparece el término
 (llamado rectangular y son consideradas lineales.
(llamado rectangular y son consideradas lineales.Algunos ejemplos de ecuaciones lineales:
Formas de ecuaciones lineales
Formas complejas como las anteriores pueden reescribirse usando las reglas del álgebra elemental en formas más simples. Las letras mayúsculas representan constantes, mientras x e y son variables.
Ecuación general-
- Aquí A y B no son ambos cero. Representa una línea en el cartesiano. Es posible encontrar los valores donde x e y se anulan.
- Ecuación segmentaria o simétrica
-
- Aquí ni E ni F no pueden ser cero. El gráfico de esta ecuación corta al eje X y al eje Y en E y F respectivamente.
- Forma paramétrica
- Dos ecuaciones que deben cumplirse de manera simultanea, cada una en la variable t. Puede convertirse a la forma general despejando t en ambas ecuaciones e igualando.
- Casos especiales:
- Un caso especial es la forma estándar donde
 y
y  . El gráfico es una línea horizontal sin intersección con el eje X ó (si F = 0) coincidente con el ese eje.
. El gráfico es una línea horizontal sin intersección con el eje X ó (si F = 0) coincidente con el ese eje.
- Otro caso especial de la forma general donde
 y
y 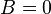 . El gráfico es una línea vertical, interceptando el eje X en E.
. El gráfico es una línea vertical, interceptando el eje X en E.
- En este caso, todas las variables fueron canceladas, dejando una ecuación que es verdadera en todos los casos. La forma original (no una tan trivial como la del ejemplo), es llamada identidad. El gráfico es todo el plano cartesiano, ya que lo satisface todo par de números reales x e y.
 .
.
Sistema de ecuaciones lineales
Los sistemas de ecuaciones lineales expresan varias ecuaciones lineales simultáneamente y admiten un tratamiento matricial. Para su resolución debe haber tantas ecuaciones como incógnitas y el determinante de la matriz ha de ser real y no nulo









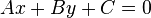





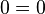

No hay comentarios:
Publicar un comentario